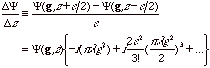8APEM, Kanazawa, 2004

Defocus Step of Through-Focus Images used to Phase Measurement in
the Transport of Intensity Equation

Kazuo Ishizuka¹, Brendan Allman²

1. HREM Research Inc, Matsukazedai, Saitama 355-0055, Japan
2. IATIA Ltd, Box Hill Nth, Vic. 3129, Australia

ishizuka@hremresearch.com

Summary
In electron microscopy many samples are phase objects. Teague showed that the phase may be determined by measuring only the intensities based on the Transport of Intensity Equation (TIE). Using the TIE we have to evaluate the differential of intensity along the wave propagation direction, which may be replaced by a difference of intensity of a series of through-focus images. We investigate in this report the focus step limit for the through-focus images, and demonstrate that we can use a sufficiently large defocus step to give sufficient intensity changes between the through-focus images. The analysis here suggests that the TIE may be applicable even to atomic resolution images.
Keywords: Transfer of Intensity Equation, Through-Focus Images, Phase measurement

In electron microscopy many samples are phase objects, for which the phase change of the incident wave is quite strong, while the modulation of amplitude may be negligible. This is the same situation in optical microscopy, where Zernike phase plate is employed in order to convert the phase modulation into the amplitude modulation to be recorded as an image intensity. In electron microscopy Scherzer [1] showed a simple defocus produces an approximate phase plate in the presence of a spherical aberration. This imaging technique has been successfully used in electron microscopy.

Teague [2] derived an equation of wave propagation (Eq. 1) in terms of the phase and the intensity in the case of small angle (paraxial) wave propagation, and showed that the phase may be determined by measuring only the intensities. We call this equation the Transport of Intensity Equation (TIE). Paganin and Nugent [3] demonstrated that the TIE can be solved in terms of pseudo-differential operator (Eq. 2), and proposed a practical solution by using Fourier transforms [4]. Van Dyck and Coene [5] obtained a similar equation in terms of the wave amplitude instead of the intensity. Using the TIE we have to evaluate the differential of intensity along the wave propagation direction, which may be replaced by a difference of intensity of a series of through-focus images. We investigate in this report the focus step limit for the through-focus images.

An accurate estimate of the intensity differential with respect to z is given in theory by a difference of intensities measured at sufficiently close image planes. However, this is not possible in practice due to non-negligible noise on the images. Therefore, larger defocused images will give a better estimate of the differential. Alas, the intensity difference with a large defocus step will give a poor estimate of the differential. Van Dyck and Coene [5] estimated an allowable limit of the focus step in their report, but mistakenly gave a wrong defocus value that is one order of magnitude smaller than the expected (0.1 nm for 0.12 nm resolution at 400 keV, it should have read 1.0 nm). Within a parabolic approximation using three data points (Figure 1) the differential of intensity at the middle plane (Eq. 3) is exactly given by an intensity difference between the first and the third images divided by their defocus difference. We may safely estimate the intensity differential, when we can accurately estimate the differential of the wave function. Then, follow the the treatment of van Dyck and Coene [5] the limit of defocus difference may be easily estimated from its Fourier transforms. This is because the effect of wave propagation in the free space is simply described by a multiplication of a well-known defocus phase change as shown in Eq. 4. Therefore, we have the expressions of the differential and the difference as shown in Eqs. 5 and 6, respectively. Estimating the differential in this way the second order term will be cancelled and the requirement for the defocus change up to resolution g is given by Eq. 7 instead of Eq. 8 used by Van Dyck and Coene. Thus, we can use a larger defocus step of 6.9 nm for the same conditions above assumed by Van Dyck and Coene. This allowable defocus step will give sufficient intensity changes between the through-focus images.

The Eqs. 1 and 5 show that the contribution of g component of the image intensity in the TIE (also the image amplitude in the case of the van Dyck formula [5]) is proportional to g^2. Therefore, low-frequency components contribute less compared with high-frequency components. However, low-frequency Fourier components of the wave function in Eq. 5 are usually stronger than the high-frequency component. Thus, we can safely estimate the whole frequency range using the TIE except very low frequencies. The analysis here suggests that the TIE may be applicable even to atomic resolution images. Some applications in material science [6, 7] as well as in biology [8] will be presented in this meeting.

References
[1] O. Schrzer, J. Appl. Phys. 20 (1949) 20-29.
[2] M.R. Teague, J. Opt. Soc. Am. 73 (1983) 1434-1441
[3] D. Paganin, K.A. Nugent, Phys. Rev. Lett. 80 (1998) 2586-2589
[4] Patent application (1999) PCT/AU99/00949.
[5] D. Van Dyck, W. Coene, Optik 77 (1987) 125-128
[6] M. Mitome, K. Ishizuka, Y.Bando, in this proceeding.
[7] M. Uchida et al., in this proceeding.
[8] H. Sawada et al., in this proceeding.
[9] The author greatly acknowledges Prof. Les Allen for valuable information.

	(Eq. 1) using the wave field of (Eq. 2) (Eq. 3) (Eq. 4) (Eq. 5) (Eq. 6) (Eq. 7) (Eq. 8)

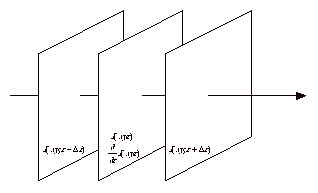
Figure 1. Three images teken with the same defocus step. The phase distribution at
the middle plane is determined from image intensities at three image planes by using
the Transport ofIntensity Equation.