Improving Energy Resolution of EELS Spectra by Deconvolution using Maximum-Entropy and Richardson-Lucy AlgorithmsKazuo Ishizuka*,**, Koji Kimoto**, Yoshio Bando*** HREM Research Inc, Matsukazedai, Saitama 355-0055, Japan ** National Institute for Materials Science, Tsukuba, Ibaraki 305-0044, Japan. Improving the energy resolution of EELS spectra acquired in TEM is very important to fully exploit the information contained in EELS near edge fine structures (ELNES). If the energy resolution is improved toward the 0.1 eV regime, ELNES details observable by EELS will open up the way for new applications. However, the energy resolution of EEL spectra is limited by the energy spread of the electron source: 0.6-0.8 eV for the Schottky field-emitter and 0.3-0.4 eV for the cold FEG. Implementation of energy monochromators has been demonstrated to improve the energy resolution down to 0.1-0.2 eV at the cost of loss of intensity [1]. An energy resolution could be improved numerically by deconvolving a core-loss spectrum by the zero-loss (or low-loss) peak. However, a simple Fourier deconvolution is apt to amplify high-frequency noise. Thus, stochastic deconvolution procedures, such as maximum-entropy (ME) [2, 3] and Richardson-Lucy (RL) [4] algorithms, have been investigated. Both algorithms do not perform a direct deconvolution, but estimate a predicted spectrum by convoluting it with the zero-loss spectrum. Therefore, they are not so much affected by noise compared with the Fourier deconvolution. It has demonstrated that an energy resolution of around 0.2-0.3 eV has been obtained with a CTEM equipped with a LaB6 gun [4]. Thus, a resolution improvement of a factor of 3-5 may be possible by applying these procedures, and resolutions of 0.2 eV and 0.1 eV could be attained using the TEM with the Schottky field-emitter and the cold FEG, respectively. We have developed a stable and easy-to-use procedure for the ME and RL algorithms using a DigitalMicrograph script language [5]. The important issues of these procedures are how to control their convergence and when we stop the processing. Therefore, there are a few parameters for each procedure that may be optimized for each spectrum to be processed. However, it may be worthwhile to note that the following results were obtained by using default parameters. We first demonstrate effectiveness of the developed procedures by using the simulated test spectrum (see Fig. 1). Both the ME and RL procedures result in almost ideal deconvolutions, even when appreciable peaks corresponding to plasmon loss are present. Next, we present in Fig. 2 a result obtained with real spectra, which are acquired from h-BN by using a Gatan GIF2002 on a Hitachi HF-3000 microscope with a cold FEG operated at 300 keV. Here, the quality of spectrum is improved by adding many measurements after adjusting spectrum position [6]. The FWHM of the p*-peak of B-K edge after deconvolution is 0.35 eV, which is close to the result obtained recently by using a TEM with a monocromator [1]. [1] P.C. Tiemeijer et al., Proc. of MSA (2001), Long Beach, CA, 1130-1131. [2] R. Kuzuo, M. Tanaka, J. of Electron Micros. 42 (1993) 240-243. [3] M.H.F. Overwijk, D. Reefman, Micron 31 (2000) 325-331. [4] A. Gloter, A. Douiri, M. Tence, C. Colliex, submitted to Ultramicroscopy. [5] Gatan R&D. [6] K. Kimoto, Y. Matsui, J. of Micorsc. 208 (2002) 224-228. [7] A part of this work was supported by "Nanotechnology Support Project" of MEXT, Japan. 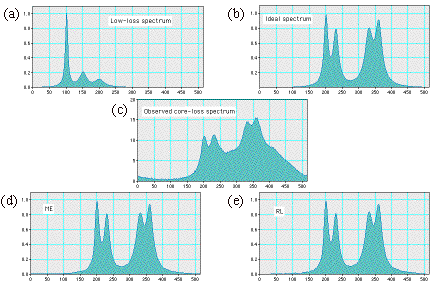 Figure 1 Testing the developed procedures using a model spectrum (c), which is obtained by convoluting an ideal spectrum (b) with a low-loss spectrum (a) and adding 0.1 background noise. The results recovered by using ME (d) (after 54 cycles) and RL (e) (after 48 cycles) are almost identical with the original spectrum. 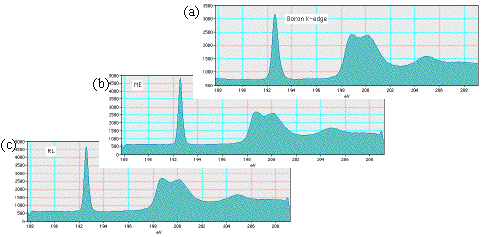 Figure 2 Deconvolution of boron K-edge (0.52 eV) taken from boron nitride (a). The FWHMs of the restored p*-peak of B-K edge for ME (b) and RL (c) are 0.35 eV (after 26 cycle) and 0.36 eV (after 18 cycle), respectively. |